lthe02_02

The state of science education is similar to that of other disciplines: research shows a clear need for new instructional strategies based on a constructivist model of learning emphasizing conceptual growth, conceptual change and the conditions that support conceptual change. Practice, however, remains anchored in behaviorist theory and rote methods of learning. “Serious constructivist approaches usually set out to reorganize traditional teaching by including changes of aims, setup of content structures, media, and teaching/learning strategies” (Treagust et al, 1996, p7). Maher and Alston (1990) discuss constructivist reform efforts and the implications for classroom teaching focusing on three issues that arise repeatedly: how to learn to listen to students’ thinking; how to organize classroom activities to support “listening and questioning”; and how to implement forms of assessment that document students’ questions.

This paper describes some constructivist teaching methodology and practices, and highlights their effectiveness as an aid to teaching and understanding in the classroom.

Over the past three decades, research on the role of students’ pre-instructional conceptions has been influenced by an old pedagogical maxim of Ausubel (1968):

The insight expressed in this dictum is of course not new in essence: it guided the work of educators, including science and mathematics educators, long before Ausubel. For example, the German educator Diesterweg (1790-1866), in his Guide for German Teachers (1835/1850), pointed out that it is of utmost importance to start instruction from the students’ point of view. He added that it is necessary therefore for the teacher to investigate students’ pre-instructional conceptions (Jung, 1993). Similarly, the hallmark of Dewey’s approach to education was the attempt to connect subject-matter knowledge with the students’ experiences. These approaches are in sharp contrast to traditional approaches that often start from facts and concepts outside the students’ range of experiences (Prawat, 1992).

Research on students’ preconceptions in science started at the end of the nineteenth century with investigations of students’ ideas of natural phenomena such as heat, frost and fire (Hall & Brown, 1903). Some forty-four years later, Oakes (1947) reviewed several hundred papers, including the landmark writings of Piaget, dealing with research on students’ ideas about natural phenomena. In the middle of the 1970’s, there began a boom of research on students’ conceptions in science and mathematics that continues today. This research focuses on investigating students’ conceptions of science and mathematics principles and concepts such as heat, energy, photosynthesis, fractions, decimals, functions, and shape. In science, 66 percent of the studies available fall into the domain of physics, with biology and chemistry sharing the remaining 34 percent (Duit,1993).

The many empirical studies provide ample evidence that students hold pre-instructional conceptions in many fields and that these are substantially different from the scientific and mathematical concepts taught in school. Most of these conceptions are held strongly and hence are very resistant to change. Research shows that students learn mathematics and science concepts and principles only to a limited degree, that sometimes students persist almost totally with their pre-instructional conceptions, and that sometimes students try to hold on to two inconsistent approaches – one intuitive and one formal. Frequently, students’ alternative conceptions are unrecognized by teachers and can affect instruction in unpredicted ways.

In the mid-1970’s, science and mathematics educators researched students’ conceptions in isolation, topic by topic. When this led to limited success in modifying students’ understandings and beliefs, researchers extended the scope of their investigations to include students’ and teachers’ beliefs about the overall scientific or mathematical enterprise, as well as their beliefs about learning and teaching. For example, philosophy of science research (Lederman, 1992; Lederman & O’Malley, 1990) has shown that students and teachers often hold rather limited views of the nature of science and mathematics. Many students and teachers are naïve realists in that they view science and mathematics knowledge as a faithful copy of the ‘world outside’ and not as a tentative human construction. Hence, teachers and students are less likely to engage in teaching and learning approaches that are based on the idea of knowledge as a tentative human construction and that usually are referred to by the term ‘constructivist’.

Students’ views of the teaching and learning process are important for learning. Many students hold a passive view and conceptualize learning as the transfer of canonical knowledge that then is stored in memory. According to this view, science is learned primarily as an accumulation of facts, and mathematics as a memorization of formulas. This view of learning as a passive process influences the students’ conceptions of what counts as legitimate work in school. Classroom discussions of alternative viewpoints and negotiated consensus are not considered a part of the ‘work’ of the classroom, and simply are viewed as wasted time that hinders efficient progress (Baird & Mitchell, 1986).

Now that research on students’ conceptions has been placed within a larger framework, including beliefs of students and teachers about knowledge, learning and teaching, the research field can inform practice about how to engage in more productive mathematics and science education. This larger framework forms the constructivist perspective.

Constructivism is described as consisting of two basic principles, one psychological and the second epistemological, and emphasizes that knowledge cannot be separated from knowing. These two principles, which make up von Glaserfeld’s (1990) radical constructivism, include many facets of Piaget’s genetic epistemology, and often serve as a reference position for discussions of constructivism in education.

The first principle states that knowledge is not received passively but is built up by the cognizing subject. In other words, it is not possible to transfer ideas into students’ heads intact; rather, students construct their own meanings from the words or visual images they hear or see. Consequently, when engaging in this construction of meaning, what the learner already knows is of central importance. This principle is becoming generally accepted by science and mathematics educators.

The second principle states that the function of cognition is adaptive and enables the learner to construct viable explanations of experiences. Consequently. Knowledge about the “world outside” is viewed as a human construction. A “reality” outside is not denied, but it is possible to know about that reality only in a personal and subjective way. This second principle is controversial for some educators, as, at first sight, it appears that it might never be possible to understand what anyone else is saying or meaning, and it might not be possible to understand the meaning that is given to what we all accept as known, particularly in science and mathematics. Rather than being concerned with knowledge as the representation of truth, constructivism focuses on the way in which learners construct viable and useful knowledge. According to this position, the only constructions that survive are those that prove to be successful in dealing with the multiple contexts in which the learner is engaged.

Researchers working from a constructivist perspective believe that knowledge is not only personally constructed but that it is also socially mediated. This third aspect highlights the fact that, although individuals have to construct their own meaning of a new phenomenon or idea, the process of constructing meaning always is embedded within the social setting of which the individual is a part.

It must be emphasized that there is no “constructivist teaching and learning,” but simply teaching and learning. According to a constructivist view, students actively construct their own knowledge whenever they learn something. However, this occurs even in settings that are not informed by constructivist ideas, that is, in strictly traditional settings in which learners are assumed to receive knowledge passively. The major difference is that constructivist teaching and learning approaches explicitly aim to help students to make the constructions that lead to understanding of the scientific or mathematical points of view. This approach is a delicate balance of students’ own activities and guidance by the teacher, or by a teaching medium such as can be provided by computers. It is obviously absurd to expect students to be able to construct science and mathematics conceptions without any guidance on the basis of their preexisting conceptions alone (Treagust et al, 1996).

In my own area of teaching, which is information systems and computing, I have been a strong advocate of constructivism, and have also strived to apply the principles for many years. I will outline here my attempts to apply these principles in two classes that I teach at Zayed University, and the results of applying constructivist principles. Prior to this however, it is important to raise the issue of standards. In a broad sense constructivism seeks to raise the standard of teaching and student understanding. No set of standards will succeed without the understanding and support of classroom teachers and several questions must be answered prior to convincing many teachers and educational authorities that constructivist teaching can define and meet these standards, particularly with regard to maintaining and exceeding the current definition of success in meeting science education guidelines using non-constructivist methodology:

Which science standards are likely to be used?
Will the science standards be used as guidelines or as a mandate for change?
What processes are in place to ensure the quality of the science standards?
What are the organizational and professional development issues to be considered?
What are the implications for curriculum and instruction?
What is the connection between assessment, accountability, curriculum, and instruction standards?
What support will be required for science programs to enable all learners to become scientifically literate?
How will we evaluate the extent and impact of implementation?
Above all, what actions must be taken to infuse the new science education standards into classroom practice (NCREL, 1994).

I would argue that the above points are vitally important for the future of constructivist teaching to succeed as a paradigm. Constructivism encompasses completely the concepts of conceptual growth and change. It is the model that guides my teaching because of the profound yet common sense concept of dealing with students’ conceptions. However, my fear is that the inherent freedom associated with the model may lend weight to the detractors of the paradigm.

It is my experience that many teachers feel comfortable with existing science courses and content organized in the traditional manner. I have heard them say that the best way to build knowledge is to collect and integrate a set of discrete facts. I suspect many favour the traditional didactic, authoritarian approach to instruction because I believe many teachers do not and will not embrace a learning model that gives students flexibility and allows them to participate in decision making. It seems to me that they accept and practice the methods that they used to acquire their knowledge and understanding of science. Advocates of the current organization of content in science usually draw heavily on a behaviorist theory of learning. Perhaps they gather these ideas from the assumption that knowledge grows from simple ideas to complex concepts, with new knowledge building on previous understanding in a predictable manner. Many of the current schooling practices are built on past learning theories that are far different from those arising from the constructivist paradigm (Marzano, 1992).

Regardless of which science standards are implemented, a new vision of science teaching and learning must be based on instruction that emphasizes engaged learning, in which students create meaning from their own experiences. Chapter two in Improving Teaching and Learning in Science and Mathematics (Treagust et al, 1996) illustrates many fine examples of how constructivism may be implemented in the classroom environment. I was particularly engaged by the work of Driver and Oldham (1986) who advocated an constructivist approach that drew on students’ existing ideas about the subject matter and, through a series of designed exercises, help them towards an understanding of an accepted model. This was an effective approach I used in one of my own classes that achieved a good level of understanding of a complex issue. I shall describe below the particular class.

The constructivist paradigm and teaching methodology in the sciences may be encapsulated by the following statements of intent:

Students will develop the skills and knowledge needed to construct their own understanding of science, technology, and the world in which they live.
Approaches to science teaching and learning will no longer be based on behaviorist thinking, but will emphasize learner-centred classrooms, problem based learning, and the construction of understanding and meaning by students.
The organization of science content will promote a more holistic view of science, rather than the traditional division of science subject matter.
Assessment will be a normal part of instruction and will help students evaluate their own learning.
Teachers will rethink their beliefs about the nature of science and science learning, resulting in a new commitment to help all students become scientifically literate.
Policymakers and administrators will break down barriers to systemic reform, such as limited time, resources, and facilities.

I would like to outline the experience I had with two fourth year computing classes at Zayed University. In teaching any subject in the local context, particularly science related subjects, there are inherent difficulties which can include a low level of English comprehension and a less than satisfactory level of scientific and mathematical understanding, which tend to hinder effective learning. I teach these female students the concepts of advanced networking and in these studies one of the most difficult concepts to understand is that of the ISO model. For purposes of clarity I have included a table of the base model below which may be referenced in conjunction with the class discussion:

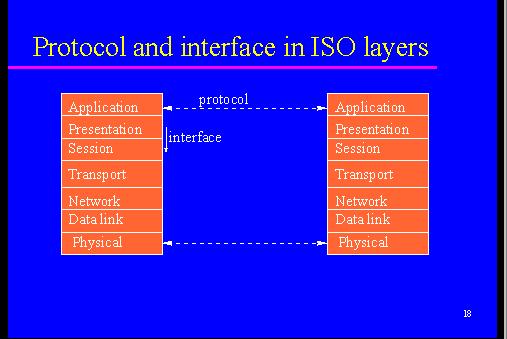
I must emphasize at this point that without a thorough understanding of the above model it is virtually impossible to understand how any network operates. This one issue has always presented many problems for teachers, and the easy solution is to tell the students to read the material and hope for the best.

Without being too technical, the central issues are as follows. Network Protocols or computer network communication protocols are a set of rules that specify the format of messages and suitable actions required for each message. The software that implements such rules are software protocols. Instead of interacting directly with hardware many applications and users interact with protocol software. Designers have chosen to divide the communication problem into subdomains that numbers each protocol, making it easier to design, implement and test. Instead of developing each protocol in isolation, protocols are designed and developed in complete sets called suites in which each protocol solves one aspect of the communication problem. The layering model is a fundamental tool that helps designers and networking professionals understand each part of the communication problem.

After two full lectures on the above model I tested the students’ understanding. It was a disaster: not one student really appreciated what happened within the model. This presented an ideal opportunity to utilize constructivism to its fullest extent utilizing problem-based learning. To create an effective learning situation in the classroom, Combs (1976) says that three characteristics are needed:

The atmosphere should facilitate the exploration of meaning. Learners must feel safe and accepted. They need to understand both the risks and rewards of seeking new knowledge and understanding. The classroom must provide for involvement, interaction, and socialization, along with a business-like approach to getting the job done.
Learners must be given frequent opportunities to confront new information and experiences in the search for meaning. However, these opportunities need to be provided in ways that allow students to do more than just receive information. Students must be allowed to confront new challenges using their past experience without the dominance of a teacher/giver of information.
New meaning should be acquired through a process of personal discovery. The methods used to encourage such personal discovery must be highly individualized and adapted to the learner’s own style and pace for learning.

I asked the students to consider a computing problem which exemplified the use of problem-based learning in a constructivist approach. I:

had identified a problem suitable for the students.
could connect the problem with the context of the students’ world so that it presented authentic opportunities.
could organize the subject matter around the problem, not the discipline.
could give the students responsibility for defining their learning experience and planning to solve the problem.
could encourage collaboration by creating learning teams.
could encourage students to demonstrate the results of their learning through a product or performance.

I split each class into eight groups of three students and I asked each group to spend 30 minutes defining the problem as they saw it. At the end of the session I asked each group to state, in their own words and in front of the class, the problem under discussion. Only two groups had at this point grasped the essentials of the problem, namely ‘stack’ communication. To guide the class I told them that in networking, communication protocols were indeed the problem but then posed the question “how does that apply to this particular problem”. I then asked the entire class if they could form a consensus that communication was the problem and after an inter-group discussion it was agreed that this was the case. However, the groups still did not have a clear idea of how to apply this consensus to the issue at hand.

I then split the class into eight groups again and posed the following question: “If there were no computers and you had to deliver a message from eight different people arranged in a hierarchy in one message, how would you do it?”. After another 20 minutes nearly all the groups said that they would do it by mail but were not clear about how the system would work. At this point I went to the stationery store and returned with eight large envelopes. The students were then split into eight groups called ‘application’, ‘presentation’, ‘session’, ‘transport’, ‘network’, ‘data-link’, ‘physical’ and ‘transmit’, in corresponding order across the room. I then told the students in ‘application’ to write a message to ‘presentation’ and seal it in an envelope. They were then asked to pass the message to ‘presentation’. The students in presentation were asked to write a message to ‘session’ and seal it in an envelope and also to include the envelope from ‘application’ in their envelope. This continued down the line until we had one envelope with ‘physical’ written on it containing seven envelopes. The question was then posed “what have we just done”. Light was dawning!, the reply was “sent a message in which we have all the stack information”. On to the next question: “fine, we have sent the message, now how do we deliver it?”. Almost immediately the envelope was passed back up the line with each group removing their envelope and reading the contents. We had just achieved real understanding of how a protocol stack works. Everyone in the class had enjoyed the exercise and I heard many girls talking about protocol stacks in ‘authoritative terms’.

This is the methodology I use to run my networking classes, I strive to make them fun and interesting. Classes that inspire interest equate to real subject matter learning. I feel that education in and on constructivist methodology should be required and necessary parts of teacher education. It is vital that we travel this route. I still regularly see many classroom situations that make me angry and frustrated, but the important thing is to ‘spread the message’.

In many countries the state of science and mathematics education is indeed parlous. This is compounded by the fact that many student teachers are opting not to be trained as science and mathematics educators. This has a circular effect in that a lack of good science and mathematics teachers results in a general lowering of science and mathematics knowledge of the students. The effect is obvious and growing.

Constructivism, I believe, offers an alternative paradigm of science teaching and learning which, if adopted and practiced, has the potential to stimulate and renew a vigorous and healthy re-emergence of interest and learning in science and mathematics.

What kind of pre-instructional ideas do your students have about your discipline?
Can you think of some key concepts in your discipline which tend to be difficult for students to grasp?
How might you apply a constructivist approach similar to that exemplified in this paper, to facilitate your students’ learning of a key concept?

Ausubel, D. P. (1968). Educational psychology: A cognitive view. New York: Holt, Rinehart and Winston.

Baird, J. R., & Mitchell, I. J. (1986). Improving the quality of teaching and learning - An Australian case study. Melbourne, Victoria: Monash University.

Combs, A. W. (1976). Fostering maximum development of the individual. In W. Van Til & K. J. Rehage (Eds.). Issues in secondary education. (NSSE Yearbook, 1976). Chicago: National Society for the Study of Education.

Driver, R., & Oldham, V. (1986). A constructivist approach to curriculum development in science. Studies in Science Education, 13, 105-122.

Duit, R. (1993). Research on students’ conceptions-Developments and trends. In J. Novak (Ed.), Proceedings of the Third International Seminar on Misconceptions and Educational Strategies in Science and Mathematics Education. Ithaca, NY: Cornell University.

Hall, G. S., & Brown, C. E. (1903). Children’s ideas of fire, heat, frost and cold. Pedagogic Seminar, 10, 27-85.

Jung, W. (1993). Uses of cognitive science in science education. Science & Education, 2, 31-56.

Lederman, N. G. (1992). Students’ and teachers’ conceptions of the nature of science: A review of research. Journal of Research in Science Teaching, 29, 331-360.

Lederman, N. G., & O’Malley, M. (1990). Students’ perceptions of tentativeness in science: Development, use, and sources of change. Science Education, 74, 225-239.

Maher, C., & Alston, A. (1990). Teacher development in mathematics in a constructivist framework. In R. Davis, C. Maher, & N. Hoddings (Eds.), Constructivist views on the teaching and learning of mathematics (pp. 147-166). Reston, VA: National Council of Teachers of Mathematics.

Marzano, R. J. (1992). A different kind of classroom: Teaching with dimensions of learning.Alexandria, VA: Association for Supervision and Curriculum Development.

National Research Council, National Committee on Science Education Standards and Assessment. (1994, November). National Science Education Standards. (Draft). Washington, DC: Author.

Oakes, M. E. (1947). Children’s explanations of natural phenomena. New York: Teachers College Press.

Prawat, R. S. (1992). Teachers’ beliefs about teaching and learning: A constructivist perspective. American Journal of Education, 100, 354-395.

Treagust, D. F., Duit, R., & Fraser, B. F. (Eds.). (1996). Improving teaching and learning in science and mathematics. New York: Teachers College Press.

Von Glaserfeld, E. (1990). An exposition on constructivism: Why some like it radical. In R. Davis, C. Maher, & N. Noddings (Eds.), Constructivist views on the teaching and learning of mathematics (Journal of Research in Mathematics Education Monograph Number 4, pp. 19-29). Reston, VA: National Council of Teachers of Mathematics.